બ્લૅક-સ્કોલ્સ મોડેલ, જે બ્લૅક-સ્કોલ્સ-મર્ટન (બીએસએમ) મોડેલ તરીકે પણ ઓળખાય છે, તે આધુનિક નાણાંકીય સિદ્ધાંતમાં એક નોંધપાત્ર ધારણા છે. આ એક ગણિત સમીકરણ છે જે સમય અને જોખમ સહિતના વિવિધ પરિબળોના આધારે વિકલ્પો કરાર જેવા ડેરિવેટિવ્સના સૈદ્ધાંતિક મૂલ્યનો અંદાજ લગાવે છે. 1973માં વિકસિત, તે કિંમતના વિકલ્પોના કરારો માટે વ્યાપક રીતે ઉપયોગમાં લેવાતી પદ્ધતિ રહે છે.
બ્લૅક-સ્કોલ્સ મોડેલની હિસ્ટ્રી
બીએસએમ મોડેલ ફિશર બ્લૅક, રોબર્ટ મર્ટન અને માયરોન સ્કોલ્સની મગજ હતી, જેમણે તેને 1973 માં રજૂ કરી હતી. વર્તમાન સ્ટૉકની કિંમતો, અપેક્ષિત ડિવિડન્ડ્સ, વિકલ્પની સ્ટ્રાઇક કિંમત, અપેક્ષિત વ્યાજ દરો, સમાપ્તિનો સમય અને અપેક્ષિત અસ્થિરતા જેવા વેરિએબલ્સનો ઉપયોગ કરીને વિકલ્પ કોન્ટ્રાક્ટના થિયોરેટિકલ મૂલ્યને નિર્ધારિત કરવા માટે તે પ્રથમ ગણિત અભિગમ હતો. આ મોડેલ કાળા અને શાળાઓ દ્વારા 1973 પેપરમાં રજૂ કરવામાં આવ્યું હતું અને પછીથી મેર્ટન દ્વારા વિસ્તૃત કરવામાં આવ્યું હતું. 1997માં, સ્કોલ્સ અને મેર્ટનને મોડેલ પર તેમના કાર્ય માટે આર્થિક વિજ્ઞાનમાં નોબલ મેમોરિયલ ઇનામ આપવામાં આવ્યું હતું.
બ્લૅક સ્કોલ્સ મોડેલ કેવી રીતે કામ કરે છે
બીએસએમ મોડેલ જાહેર કરે છે કે સ્ટૉક્સ અથવા ફ્યુચર્સ કોન્ટ્રાક્ટ્સ જેવા ફાઇનાન્શિયલ ઇન્સ્ટ્રુમેન્ટ્સ, સતત ડ્રિફ્ટ અને અસ્થિરતા સાથે રેન્ડમ વૉકને અનુસરીને કિંમતોનું અસામાન્ય વિતરણ પ્રદર્શિત કરશે. મોડેલમાં પાંચ વેરિએબલની જરૂર છે: અસ્થિરતા, અંતર્નિહિત સંપત્તિની કિંમત, વિકલ્પની સ્ટ્રાઇક કિંમત, વિકલ્પની સમાપ્તિ સુધીનો સમય અને જોખમ-મુક્ત વ્યાજ દર. આ વેરિએબલ્સ સાથે, મોડેલ યુરોપિયન-સ્ટાઇલ કૉલ વિકલ્પની કિંમતની ગણતરી કરે છે.
બ્લૅક-સ્કોલ્સની ધારણા
બ્લૅક સ્કોલ્સ મોડેલ ઘણી ધારણાઓ કરે છે:
- વિકલ્પના જીવન દરમિયાન કોઈ ડિવિડન્ડ ચૂકવવામાં આવતા નથી.
- માર્કેટ રેન્ડમ છે, એટલે કે માર્કેટમાં હલનચલનની આગાહી કરી શકાતી નથી.
- વિકલ્પ ખરીદવામાં કોઈ ટ્રાન્ઝૅક્શન ખર્ચ નથી.
- અંડરલાઈંગ એસેટનો જોખમ-મુક્ત દર અને અસ્થિરતા જાણીતા અને સ્થિર છે.
- અંડરલાઈંગ એસેટનું વળતર સામાન્ય રીતે વિતરિત કરવામાં આવે છે.
- આ વિકલ્પ યુરોપિયન છે અને ફક્ત સમાપ્તિ પર જ તેનો ઉપયોગ કરી શકાય છે.
ધ બ્લૅક સ્કોલ્સ મોડેલ ફોર્મ્યુલા
સંચિત ધોરણે સામાન્ય સંભાવના વિતરણ કાર્ય દ્વારા શેરની કિંમતને ગુણાકાર કરીને બ્લૅક સ્કોલ્સ ફોર્મ્યુલાની ગણતરી કરવામાં આવે છે. ત્યારબાદ, સંચિત ધોરણે સામાન્ય વિતરણ દ્વારા ગુણાકાર સ્ટ્રાઇક પ્રાઇસનું નેટ પ્રેઝન્ટ વેલ્યૂ (એનપીવી) અગાઉની ગણતરીના પરિણામી મૂલ્યથી ઘટાડવામાં આવે છે.
અહીં તેનું ગણિત પ્રતિનિધિત્વ કરવામાં આવ્યું છે:
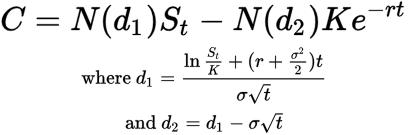
ક્યાં,
સી = કૉલ વિકલ્પની કિંમત
એન = સામાન્ય વિતરણના સીડીએફ
એસટી = એસેટની સ્પૉટ કિંમત
કે = સ્ટ્રાઇક પ્રાઈઝ
આર = જોખમ-મુક્ત વ્યાજ દર
ટી = મેચ્યોરિટીનો સમય
એન= સંપત્તિની અસ્થિરતા
બ્લૅક-સ્કોલ્સ મોડેલના લાભો
- તે કિંમતના વિકલ્પો માટે સૈદ્ધાંતિક રૂપરેખા પ્રદાન કરે છે, જે રોકાણકારો અને વેપારીઓને માળખાગત, વ્યાખ્યાયિત પદ્ધતિનો ઉપયોગ કરીને વિકલ્પની યોગ્ય કિંમત નિર્ધારિત કરવાની મંજૂરી આપે છે.
- તે રોકાણકારોને વિવિધ સંપત્તિઓ માટે તેમના જોખમ એક્સપોઝરને સમજવાની મંજૂરી આપીને રિસ્ક મેનેજમેન્ટને સક્ષમ બનાવે છે.
- તેનો ઉપયોગ વિવિધ વિકલ્પો સાથે સંકળાયેલા અપેક્ષિત રિટર્ન અને જોખમોના માપ ઉપલબ્ધ કરીને પોર્ટફોલિયો ઑપ્ટિમાઇઝેશન માટે કરી શકાય છે.
- તે બજારની કાર્યક્ષમતા અને પારદર્શિતા વધારે છે કારણ કે વેપારીઓ અને રોકાણકારો કિંમત અને વેપારના વિકલ્પોમાં વધુ સારા છે.
- તે કિંમતને સુવ્યવસ્થિત કરે છે, જે વિવિધ બજારો અને અધિકારક્ષેત્રોમાં વધુ સાતત્ય અને તુલના કરવાની મંજૂરી આપે છે.
બ્લૅક સ્કોલ્સ મોડેલ રોકાણકારોને કેવી રીતે લાભ આપી શકે છે તેના કેટલાક વિશિષ્ટ ઉદાહરણો અહીં આપેલ છે:
- વિકલ્પની યોગ્ય કિંમત નિર્ધારિત કરવા માટે. બ્લૅક-સ્કોલ્સ મોડેલનો ઉપયોગ વિકલ્પની સૈદ્ધાંતિક કિંમતની ગણતરી કરવા માટે કરી શકાય છે, જેનો ઉપયોગ બજાર કિંમતની તુલનામાં કરી શકાય છે કે વિકલ્પનું મૂલ્ય ઓછું છે કે નહીં.
- જોખમ સામે રક્ષણ આપવું. એક વિકલ્પ ખરીદીને, કોઈ રોકાણકાર પોતાને અંતર્નિહિત સંપત્તિ કિંમત પડવાના જોખમ સામે સુરક્ષિત કરી શકે છે. ઉદાહરણ તરીકે, જો કોઈ રોકાણકાર કંપનીમાં શેરની માલિકી ધરાવે છે, તો તેઓ એક ચોક્કસ સ્તરની નીચે આવતા શેર કિંમતના જોખમ સામે પોતાને સુરક્ષિત કરવા માટે તે શેર પર એક મૂકવાનો વિકલ્પ ખરીદી શકે છે.
- ટ્રેડિંગ વ્યૂહરચનાઓ બનાવવા માટે. અન્ય નાણાંકીય સાધનો સાથે વિકલ્પોને જોડીને, રોકાણકારો વિવિધ બજાર સ્થિતિઓમાં નફા ઉત્પન્ન કરવા માટે વ્યૂહરચનાઓ બનાવી શકે છે.
બ્લૅક-સ્કોલ્સ મોડેલની મર્યાદા
તેના લાભો હોવા છતાં, બ્લૅક-સ્કોલ્સ મોડેલમાં કેટલીક મર્યાદા છે:
- તેનો ઉપયોગ ફક્ત યુરોપિયનના વિકલ્પોની કિંમત માટે કરવામાં આવે છે અને એ હકીકત માટે જ કરવામાં આવતો નથી કે સમાપ્તિની તારીખ પહેલાં અમેરિકન વિકલ્પોનો ઉપયોગ કરી શકાય છે.
- તે માને છે કે ડિવિડન્ડ અને જોખમ-મુક્ત દરો સ્થિર છે, જે હંમેશા કેસ ન હોઈ શકે.
- તે માને છે કે વિકલ્પના જીવન પર અસ્થિરતા સ્થિર રહે છે, જે ઘણીવાર કેસ નથી હોતી કારણ કે અસ્થિરતા સપ્લાય અને માંગના સ્તર સાથે વધતી જાય છે.
- તે અન્ય ઘણી ધારણાઓ કરે છે, જેમ કે કોઈ ટ્રાન્ઝૅક્શન ખર્ચ અથવા કર, તમામ પરિપક્વતાઓ માટે સતત જોખમ-મુક્ત વ્યાજ દરો અને કોઈ જોખમરહિત માધ્યસ્થમ તકો નથી. આ ધારણાઓ વાસ્તવિક પરિણામોથી વિચલિત કિંમતો તરફ દોરી શકે છે.
- આ એક "બ્લૅક બૉક્સ" મોડેલ છે. આનો અર્થ એ છે કે આ મોડેલ તેના પરિણામો પર કેવી રીતે આવે છે તે હંમેશા સ્પષ્ટ નથી. આ ઑપ્શન કિંમતોને અસર કરતા અંતર્નિહિત પરિબળોને સમજવા માટે મોડેલનો ઉપયોગ કરવું મુશ્કેલ બનાવી શકે છે.

